Multi-scale approaches
The scale space representation of a signal obtained by Gaussian smoothing satisfies a number of special properties, scale-space axioms, which make it into a special form of multi-scale representation. There are, however, also other types of "multi-scale approaches" in the areas of computer vision, image processing and signal processing, in particular the notion of wavelets. The purpose of this article is to describe a few of these approaches:
Scale-space theory for one-dimensional signals
For one-dimensional signals, there exists quite a well-developed theory for continuous and discrete kernels that guarantee that new local extrema or zero-crossings cannot be created by a convolution operation.[1] For continuous signals, it holds that all scale-space kernels can be decomposed into the following sets of primitive smoothing kernels:
- the Gaussian kernel :
 where
where  ,
, - truncated exponential kernels (filters with one real pole in the s-plane):
 if
if  and 0 otherwise where
and 0 otherwise where 
 if
if  and 0 otherwise where
and 0 otherwise where  ,
,
- translations,
- rescalings.
For discrete signals, we can, up to trivial translations and rescalings, decompose any discrete scale-space kernel into the following primitive operations:
- the discrete Gaussian kernel
 where
where  where
where 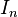 are the modified Bessel functions of integer order,
are the modified Bessel functions of integer order,
- generalized binomial kernels corresponding to linear smoothing of the form
 where
where 
 where
where  ,
,
- first-order recursive filters corresponding to linear smoothing of the form
 where
where 
 where
where  ,
,
- the one-sided Poisson kernel
 for
for  where
where 
 for
for  where
where  .
.
From this classification, it is apparent that it we require a continuous semi-group structure, there are only three classes of scale-space kernels with a continuous scale parameter; the Gaussian kernel which forms the scale-space of continuous signals, the discrete Gaussian kernel which forms the scale-space of discrete signals and the time-causal Poisson kernel that forms a temporal scale-space over discrete time. If we on the other hand sacrifice the continuous semi-group structure, there are more options:
For discrete signals, the use of generalized binomial kernels provides a formal basis for defining the smoothing operation in a pyramid. For temporal data, the one-sided truncated exponential kernels and the first-order recursive filters provide a way to define time-causal scale-spaces [2][3] that allow for efficient numerical implementation and respect causality over time without access to the future. The first-order recursive filters also provide a framework for defining recursive approximations to the Gaussian kernel that in a weaker sense preserve some of the scale-space properties.[4][5]
See also
References
- ↑ Lindeberg, T., "Scale-space for discrete signals," PAMI(12), No. 3, March 1990, pp. 234-254.
- ↑ Richard F. Lyon. "Speech recognition in scale space," Proc. of 1987 ICASSP. San Diego, March, pp. 29.3.14, 1987.
- ↑ Lindeberg, T. and Fagerstrom, F.: Scale-space with causal time direction, Proc. 4th European Conference on Computer Vision, Cambridge, England, April 1996. Springer-Verlag LNCS Vol 1064, pages 229--240.
- ↑ Young, I.I., van Vliet, L.J.: Recursive implementation of the Gaussian filter, Signal Processing, vol. 44, no. 2, 1995, 139-151.
- ↑ Deriche, R: Recursively implementing the Gaussian and its derivatives, INRIA Research Report 1893, 1993.